Rotting Oranges | Minimum Time required to rot all oranges in a box | Leetcode 994

In this article, I am explaining the optimal approach to solve the minimum time required to rot all the fresh oranges in given box of oranges.

‘Rotting oranges’ problem is about finding whether all the oranges in a matrix or box is rotten because of presence of one or more rotten oranges in the box. Sometimes, there can be no rotten oranges. Sometimes there can be one or more rotten oranges. The rotten oranges are represented by 2 in matrix, fresh oranges are represented by 1 in matrix, 0 means no orange is present there.

If there are no rotten oranges in the box, the final answer is 0, because no oranges has been changed from fresh to rotten. If there are 1 or more rotten oranges in the box, check which oranges becomes changed from fresh to rotten (1->2). The final answer is checking if no fresh oranges with value 1 are there in box. If there is any fresh orange (1), then print answer as ‘-1’. If all the oranges present in the box are rotten (2), find in how many minutes all the fresh oranges became rotten in the box.

• 0 = No oranges
• 1 = Fresh orange
• 2 = Rotten orange

Actual goal: Finding "minimum time" required for all the fresh oranges in the box to rot?

So, the oranges’ position is represented as 2D matrix. We know that we should start from any rotten oranges and penetrate to nearby oranges which are valid and fresh (1) in 4 directions(left, right, top, bottom). But which traversal algorithm can be used: DFS or BFS?

Here we can use BFS. Because from every rotten oranges, we are checking its nearby fresh orange cells, and adding them to a queue to check again their nearby 4 sides. This goes on and on. As we start checking all the nearby 4 direction cells initially How fresh oranges rot? By coming in contact with a nearby rotten orange cell. So, this is shorter or nearby based cells. This can be taken as level by level checking of fresh oranges. Hence, BFS (Breadth First Traversal) can be used.

How to calculate time to rot?

Initially when adding all the rotten oranges to queue, the time is 0. Then after adding each set of nearby valid cells to the queue, the counter ‘count’ is incremented. This denotes how much time we transformed all possible fresh oranges to rot. The variable ‘rotten’ keeps count of how many fresh oranges have been transformed to rotten oranges in the process. This variable helps in determining the final answer.

🍊If any one orange is fresh in the box finally, then print “-1” as answer. This means that a fresh orange is unable to rot in the box. Or it means it is untouched by rotten orange.
🍊If all the oranges are rotten finally in the box, check the ‘rotten’ count. If rotten=0, then it means that no oranges have been transformed from fresh to rotten. So, print 0 as answer.
🍊Else all oranges are rotten in the box and also if rotten is greater than 0, print the ‘count’ value subtracted by 1 as answer.

Example with explanation:

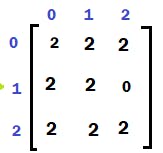
Let us walk through an example below: mat = {{2,1,1},{1,1,0},{0,1,1}}. Find the minimum time required to rot all oranges in given matrix.

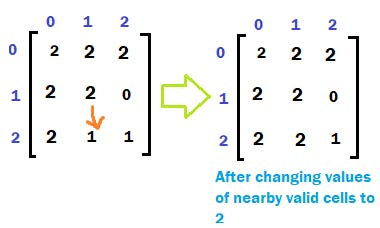
Initially this is the box with oranges. This can be represented in matrix as below:

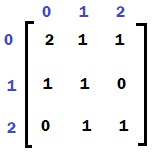
Solution: Using queue data structure, first adding all the rotten oranges in the box. So, add all cells with value 2 in the matrix to the queue. The cell is added as its (row, column) format.

Step 1: Initially the queue is empty. After adding all rotten oranges from box, the queue is as below:

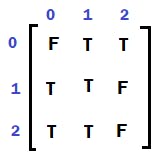
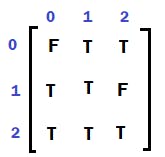
Using a boolean 2D array ‘visited’ to mark which cells in the matrix are visited or not visited. It is as below:

Step 2: Poll all the elements from the queue one by one. And check the 4 sides of the polled element if they are valid and fresh orange (1) and not visited. If the side is valid and not visited, add it to the queue. Now initially checking the queue with time=count=0. Count is incremented, now count=1. Loop through all the elements which are now present in queue. Now queue size is 1, hence loop only once. Poll from queue, cell [0,0] is polled. Now the current element is [0,0].

Check all the 4 sides of this current element.

Left = [row,column-1] = [0,0–1] = [0,-1] out of bound

Right = [row,column+1] = [0,0+1] = [0,1]

Top = [row-1,column] = [0–1,0] = [-1,0] out of bound

Bottom = [row+1,column] = [0+1,0] = [1,0]

Here, the left and top sides are invalid because they are out of the boundary of the matrix size. Check the remaining sides: Right and bottom sides are valid because they are within the boundary, and also fresh with value 1, and not visited because,

Visited[right] = visited[0,1] = false,

Visited[bottom] = visited[1,0] = false.

Hence add these nearby valid cells right and bottom to the queue.

Change the value of these valid cells to 2 denoting that they have rotten now. Hence, matrix[0][1] = 2, and matrix[1][0] = 2.

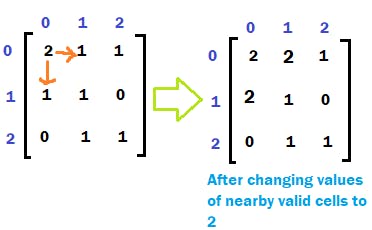
Also, mark in the boolean visited array for these valid cells as TRUE.

As there are two valid cells from the current element [0,0], increment ‘rotten’ value by 2. Rotten = rotten+2 = 0+2 = 2 In 1 minute the oranges rotten are as below:

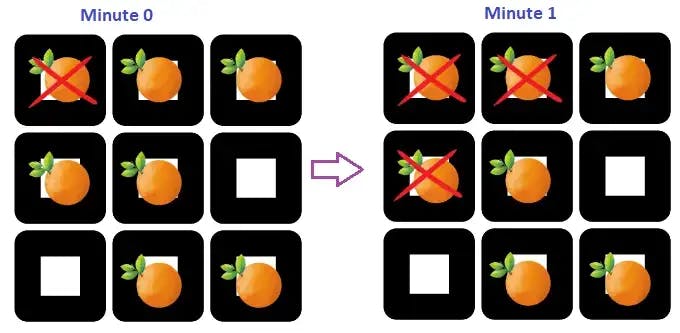
As per the ‘len’ size, only one element have been polled from the queue. Loop through while loop again.

Step 3: Check if the queue is empty or not. No, queue is not empty. So, Count is incremented, now count=1.

Count = count+1 = 1+1 = 2

Loop through all the elements which are now present in the queue. Now queue size is 2, hence iterate two times and poll the queue two times.

=> Polling from the queue. Polled [0,1]. Now the current element is [0,1]. Check all the 4 sides of this current element.

Left = [row,column-1] = [0,1–1] = [0,0]

Right = [row,column+1] = [0,1+1] = [0,2]

Top = [row-1,column] = [0–1,0] = [-1,0] out of bound house

Bottom = [row+1,column] = [0+1,1] = [1,1]. Here, the top side is invalid because it is out of the boundary of the matrix size. Check the remaining sides: left, right, bottom.

Left is not valid because it is not fresh orange, it is rotten orange with value 2. Already rotten oranges need not be rotten again. So, left side cell is invalid. Right, bottom sides are valid because they are within the boundary, and also fresh with value 1, and not visited because:

Visited[right] = visited[0,1] = false

Visited[bottom] = visited[1,0] = false

Hence add these nearby valid cells right and bottom to the queue.

Change the value of these valid cells to 2 denoting that they have rotten now. Hence, matrix[0][2] = 2, and matrix[1][1] = 2.

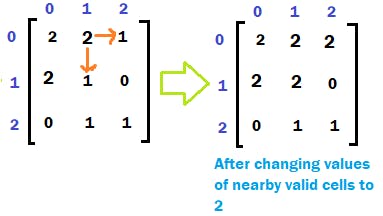
Also, mark in boolean visited array for these valid cells as TRUE.

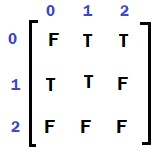
As there are two valid cells from the current element [0,1], increment ‘rotten’ value by 2.

Rotten = rotten+2 = 2+2 = 4

The transformation from fresh to rotten oranges in time frame 2 is as below:

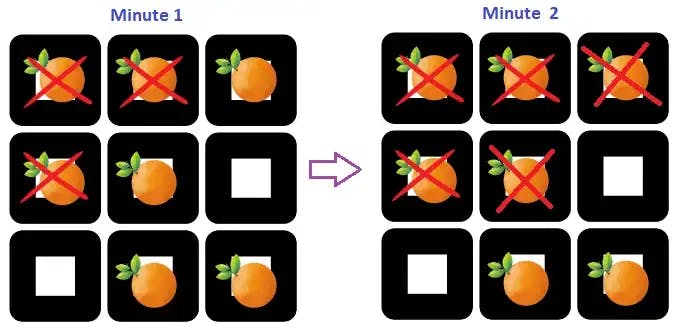
As per the ‘len’ size=2, only one element have been polled from the queue. Iterating again and polling again from the queue.

=> Polling from the queue. Polled [1,0]. Now the current element is [1,0].

Check all the 4 sides of this current element.

Left = [row,column-1] = [1,0–1] = [1,-1] out of bound

Right = [row,column+1] = [1,0+1] = [1,1]

Top = [row-1,column] = [1–1,0] = [0,0]

Bottom = [row+1,column] = [1+1,0] = [2,0]

Here, the left side is invalid because it is out of the boundary of the matrix size. Check the remaining sides: top, right, bottom.

Top, right are not valid because they are not fresh oranges, it is rotten orange with value 2. Already rotten oranges need not be rotten again. So, top and right side cells are invalid.

Bottom side is not valid because they are within the boundary, and empty.

Hence not adding these nearby valid cells to the queue.

As per the ‘len’ size=2, two elements have been polled from the queue.

Step 4: Check if the queue is empty or not. No, queue is not empty. So, Count is incremented, now count=2.

Count = count+1 = 2+1 = 3

Loop through all the elements which are now present in the queue. Now queue size is 2, hence iterate two times and poll the queue two times.

Check all the 4 sides of this current element.

Left = [row,column-1] = [0,2–1] = [0,1]

Right = [row,column+1] = [0,2+1] = [0,3] out of bound

Top = [row-1,column] = [0–1,2] = [-1,2] out of bound

Bottom = [row+1,column] = [0+1,2] = [1,2]

Here, the right and top side is invalid because it is out of the boundary of the matrix size. Check the remaining sides: left, bottom.

Left is not valid because they are not fresh oranges, it is rotten orange with value 2. Already rotten oranges need not be rotten again. So, left side cell is invalid.

Bottom side is also not valid because they are within the boundary, but empty with value 0. Hence no cells nearby are valid. Pop the queue again if not empty.

=> Polling from the queue. Polled [1,1]. Now the current element is [1,1].

Check all the 4 sides of the current element.

Left = [row,column-1] = [1,1–1] = [1,0]

Right = [row,column+1] = [1,1+1] = [1,2]

Top = [row-1,column] = [1–1,1] = [0,1]

Bottom = [row+1,column] = [1+1,2] = [2,1]

Here top, left, right are not valid because they are not fresh oranges, they are rotten oranges with value 2. Already rotten oranges need not be rotten again. So, these side cells are invalid.

Bottom cell is only valid because it is within the boundary, and also fresh orange with value 1. It is marked as FALSE as not visited.

Visited[bottom] = visited[2,1] = false

Hence add these nearby valid cell bottom to the queue.

Change the value of these valid cells to 2 denoting that they have rotten now. Hence, matrix[2][1] = 2.

Also, mark in boolean visited array for these valid cells as TRUE.

As only one cell is valid nearby, increment ‘rotten’ value by 1.

Rotten = rotten+1 = 4+1 =5

The transformation of fresh oranges to rotten in time frame 3 is as below:

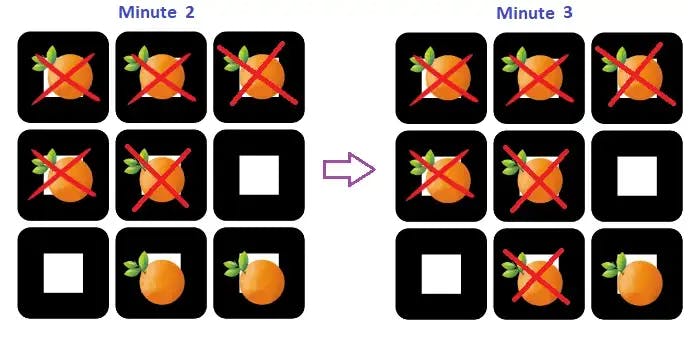
As the ‘len’ size, the queue is polled two times. Next, check if the queue is empty or not and pop again.

Step 5: Check if the queue is empty or not. No, the queue is not empty. So, Count is incremented, now count=3.

Count = count+1 = 3+1 = 4

Iterate through all the elements which are present in the queue now. Now the queue size is 1. Hence, iterate only once and poll the queue once.

=> Poll from the queue. Polled [2,1]. Now the current element is [2,1].

Check all the 4 sides of the current element.

Left = [row,column-1] = [2,1–1] = [2,0]

Right = [row,column+1] = [2,1+1] = [2,2]

Top = [row-1,column] = [2–1,1] = [1,1]

Bottom = [row+1,column] = [2+1,1] = [3,1] out of bound

Here the bottom is invalid because it is out of bound. The other sides top and left are invalid because they are already rotten with value 2 in the matrix. The side right is only valid, because it is within boundary and fresh with value 1.

Add right cell to the queue.

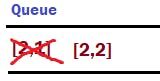
Change the value of these valid cells to 2 denoting that they have rotten now. Hence, matrix[2][2] = 2.

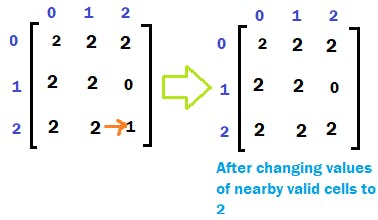
Also, mark in the boolean visited array for these valid cells as TRUE.

As there is one valid cells from the current element [2,1], increment ‘rotten’ value by 1.

Rotten = rotten+2 = 5+1 = 6

The transformation of fresh to rotten oranges in time 4 is as below:

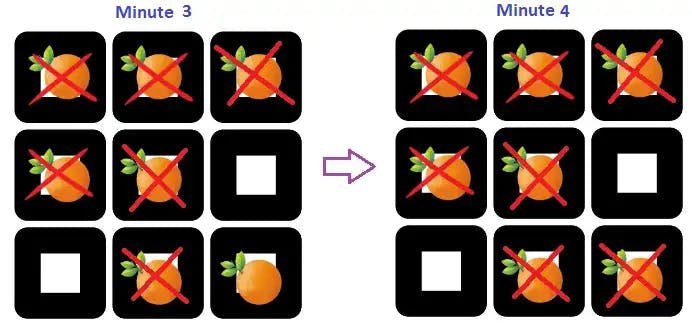
As per the ‘len’ size, only one element have been polled from the queue.

Step 6: Check if the queue is empty or not. No, queue is not empty. So, Count is incremented, now count=4.

Count = count+1 = 4+1 = 5

=> Poll from the queue. Polled [2,2]. Now the current element is [2,2].

Check all the 4 sides of the current element.

Left = [row,column-1] = [2,2–1] = [2,1]

Right = [row,column+1] = [2,2+1] = [2,3] out of bound

Top = [row-1,column] = [2–1,2] = [1,2]

Bottom = [row+1,column] = [2+1,2] = [3,1] out of bound

Here only the left and top are within the boundary, but they are not valid because they are already rotten.

So, no cells are valid and no cells are added to the queue. As the ‘len’ size, the queue is polled one time. Next, check if the queue is empty or not and pop again.

Step 7: Check if the queue is empty or not. YES, the queue is empty.

Now no more iteration is required as the queue is empty. Next, check if there is one or more fresh oranges in the matrix.

Check if there is any value 1 in the matrix. No, the matrix has no values as 1, means it has no fresh oranges in the matrix now.

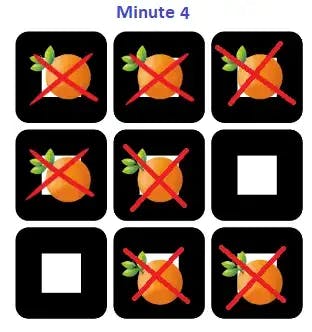
Hence, next check if the ‘rotten’ value is greater than 0. Rotten=6 now, hence we can confirm that some oranges have been transformed from fresh to rotten within time frame. So, print the ‘count-1’ value as the time took for fresh oranges to rot in the box.

Here, count=5. So, time took to rot = count-1

= 5–1 = 4

This means that in 4 minutes all the fresh oranges are rotten.

Code snippet in Java:

class Solution {
    class Pair{
        int x, y;
        Pair(int x,int y){
            this.x = x;
            this.y = y;
        }
        public int getX(){
            return x;
        }
        public int getY(){
            return y;
        }
    }
    public int orangesRotting(int[][] grid) {
        boolean[][] visited = new boolean[grid.length][grid[0].length];
        Queue<Pair> q = new LinkedList<>();
        int countFreshOranges=0;
        for(int outerindex=0;outerindex<grid.length;outerindex++){
            for(int innerindex=0;innerindex<grid[outerindex].length;innerindex++){
                if(grid[outerindex][innerindex]==2){
                    q.add(new Pair(outerindex,innerindex));
                    visited[outerindex][innerindex]=true;
                }
                if(grid[outerindex][innerindex]==1){
                    countFreshOranges++;
                }
            }
        }
        int[] xplane = {0,0,1,-1};
        int[] yplane = {-1,1,0,0};
        int time=0, rotten=0;
        while(!q.isEmpty()){
            int len = q.size();
            time++;
            for(int k=0;k<len;k++){
                Pair curr = q.poll();
                int currX = curr.getX();
                int currY = curr.getY();
                for(int side=0;side<4;side++){
                    if(isValid(currX+xplane[side],currY+yplane[side],visited,grid)){
                        grid[currX+xplane[side]][currY+yplane[side]]=2;
                        visited[currX+xplane[side]][currY+yplane[side]]=true;
                        q.add(new Pair(currX+xplane[side],currY+yplane[side]));
                        rotten++;
                    }
                }
            }
        }
        if(rotten<countFreshOranges){
            return -1;
        }
        if(rotten==0){
            return 0;
        }
        return time-1;
    }
    public boolean isValid(int x,int y,boolean[][] visited,int[][] grid){
        if(x<grid.length && x>=0 && y<grid[0].length && y>=0 && visited[x][y]==false && grid[x][y]==1){
            return true;
        }
        return false;
    }
}

Time complexity: O(M*N) where M is the number of rows in matrix and N is the number of columns in the matrix.

Space complexity: O(M*N) where M is the number of rows in matrix and N is the number of columns in the matrix. Because to store all the elements in the queue from the matrix, it takes O(M*N) space, if suppose all the elements are rotten in the matrix in worst case.

Thanks for reading!